
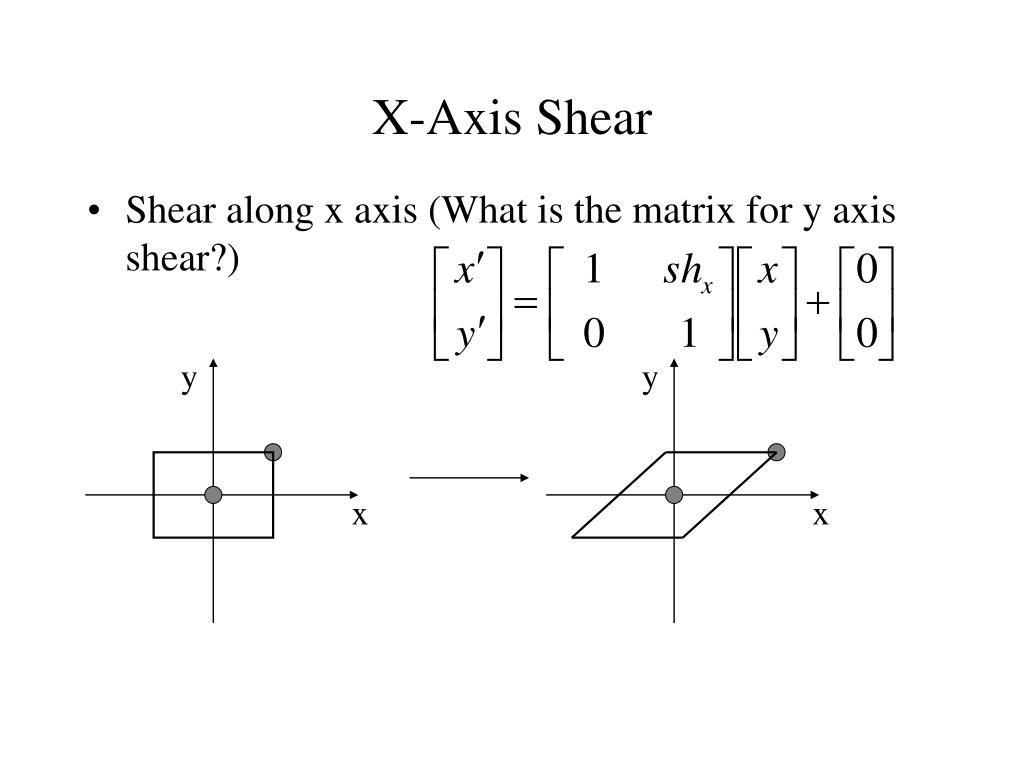
So the intersection of the two lines is the point C(51/50, 457/50). Now we need to find the intersection of the lines y = 7x + 2 and y = (-1/7)x + 65/7 by solving this system of equations. Thus, you are looking for a matrix multiplication that will yield the. Math Definition: Reflection Over the Y Axis. So the equation of this line is y = (-1/7)x + 65/7. In a reflection over the x-axis, the x-coordinates of the image will be the same. Heres how I would do that problem: Any 2 by 2 matrix can be written as. In this section, we will examine some special examples of linear transformations in R2 including rotations and reflections. So the desired line has an equation of the form y = (-1/7)x + b. Find the matrix of rotations and reflections in R2 and determine the action of each on a vector in R2. Since the line y = 7x + 2 has slope 7, the desired line (that is, line AB) has slope -1/7 as well as passing through (2,9).
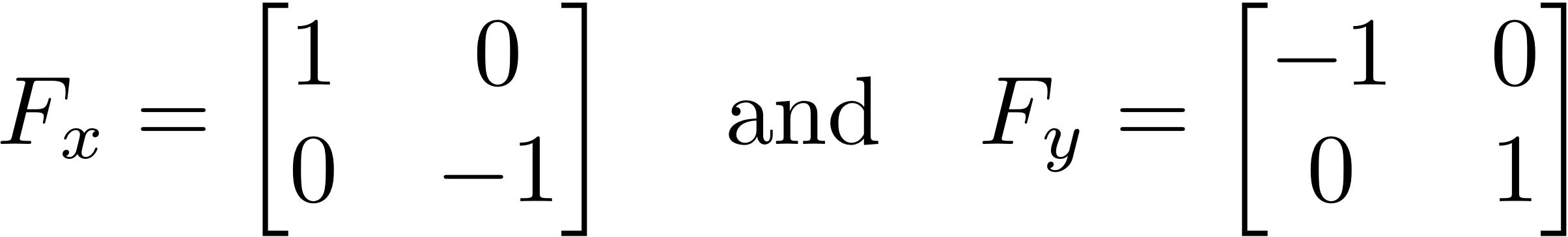
So we first find the equation of the line through (2,9) that is perpendicular to the line y = 7x + 2. reflection across the vertical axis is represented by the matrix equation.
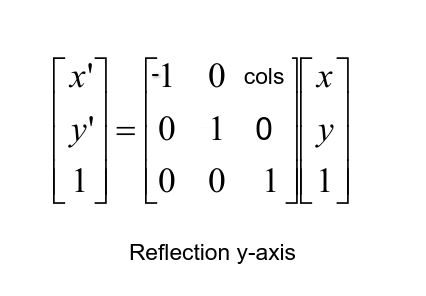
Then, using the fact that C is the midpoint of segment AB, we can finally determine point B.Įxample: suppose we want to reflect the point A(2,9) about the line k with equation y = 7x + 2. In coordinates, this means that the image has the same y-coordinate as the. Then we can algebraically find point C, which is the intersection of these two lines. So we can first find the equation of the line through point A that is perpendicular to line k. Note that line AB must be perpendicular to line k, and C must be the midpoint of segment AB (from the definition of a reflection). Let A be the point to be reflected, let k be the line about which the point is reflected, let B represent the desired point (image), and let C represent the intersection of line k and line AB. This video explains what the transformation matrix is to reflect in the y-axis.


 0 kommentar(er)
0 kommentar(er)
